Self-attention is a softmax function, it does not model position information. Paper Self-Attention with Relative Position Representations proposed a method on how to incorporate relative position in self-attention.
What is self-attention?
There are some methods to implement self-attention. This paper proposed one.
For example:
\(x = (x_1, . . . , x_n)\) is a sequence with \(n\) elements where \(x_i\in R^{d_x}\), and computes a new sequence \(z = (z_1, . . . , z_n)\) of the same length where \(z_i\in R^{d_z}\).
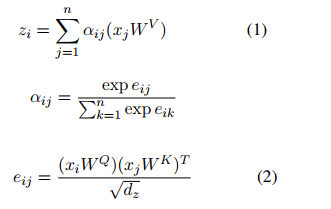
As to this kind of self-attention, we will get a attention score matrix with n*n. Here \(W^Q\), \(W^K\) and \(W^V \in R^{d_x * d_z}\) are trainable parameters.
What is relative position representations?
Relative position representations are defined based on a target, for example \(x_i\) in a sentence. In order to determine relative position representations, we should know how to compute relative position based on \(x_i\).
For example, \(x\) is the target, we can use equation below to compute relative postion.
clip(x, k) = max(−k, min(k, x))
Then we can create relation postion representations as below:

How to incorporate relative position representations in self-attention?
Here is the computation:
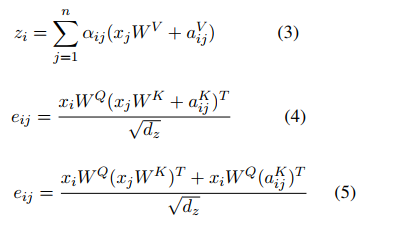
Here \(a^V_{ij}\) is the relative position representations \(x_j\) to target \(x_i\).