SimCLR directly maximizes the similarity between augmented positive pairs and minimizes the similarity of negative pairs via a contrastive InfoNCE loss in the latent space. For a mini-batch of \(N\) samples, we can get \(2N\) samples after augmentation. SimCLR doesn’t sample negative examples explicitly. The \(2(N − 1)\) samples different from the positive pair are treated as negative examples. The loss function is defined as,
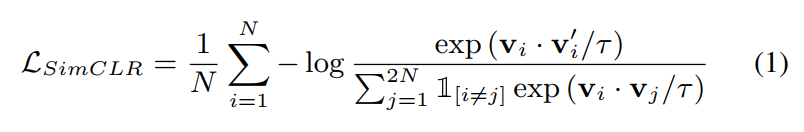
where \(v_i\) and \(v_i^’\) are the two augmentations of one sample, \(v_j\) is from the rest \(2N − 1\) augmented samples, \(1_{[i = j]}\) is an indicator function that equals to 1 when \(i \neq j\). τ is the temperature parameter. Our above definition is slightly different from the original SimCLR implementation, which also swaps sample \(v_i\) and \(v_i^’\) and calculates an average loss.
Reference
Aaron van den Oord, Yazhe Li, and Oriol Vinyals, “Representation learning with contrastive predictive coding,” arXiv preprint arXiv:1807.03748, 2018.