SimCLR uses samples in the current mini-batch for negative example mining. The negative sample size is constrained with the minibatch size \(N\), which is limited by the GPU memory. To prevent this problem and introduce more negative samples in the InfoNCE loss, we also explore a momentum contrastive based speaker embedding system. We mainly follow the MoCo framework for visual representation learning. MoCo uses a dynamic queue to sample a large number of negative samples to calculate the loss with an assumption that robust features can be learned by a large dictionary that covers a rich set of negative samples. Illustrated in Fig. 1,
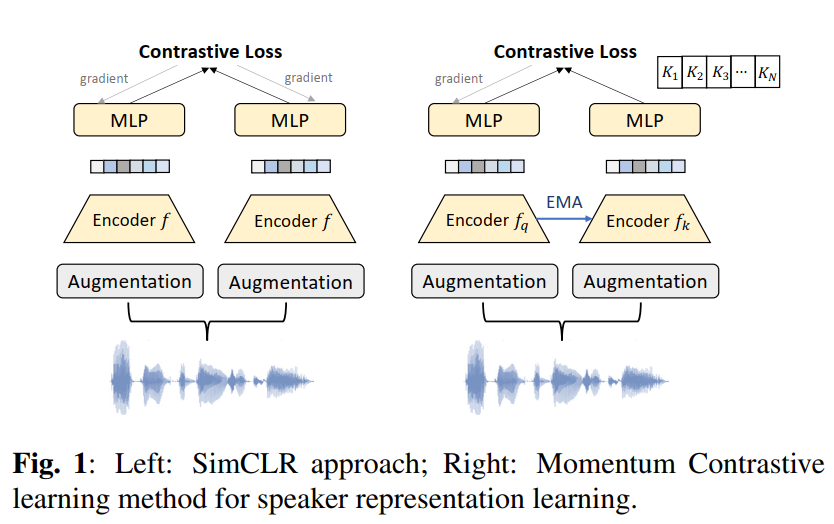
one major difference between MoCo and SimCLR is that MoCo uses one query encoder (left) to encode one copy of the augmented samples, and employs a momentum encoder (right) to encode the other copy. So the InfoNCE loss employed in the momentum contrastive speaker embedding learning is defined as,
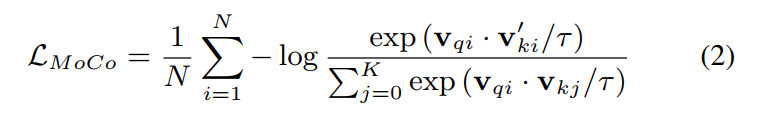
where \(v_{qi}\) and \(v_{ki}^`\) is one of the query samples (i.e., anchor) and corresponding key samples (i.e., positive) in the mini-batch. \(v_{kj}\) are the key samples encoded with the key encoder (momentum encoder), the sum in Eq. (2) is over one positive pair and K negative pairs. The introduction of a queue with the dictionary size K is able to enlarge the number of negative samples compared with the
original InfoNCE. At the same time, samples in the dictionary are progressively replaced. K can be 1000 or 10000 in experiments. When
the current mini-batch is enqueued to the dictionary, the oldest minibatch will be dequeued.
To make the key embeddings in the negative queue consistent, the key encoder \(f_k\) is updated as an Exponential Moving Average
(EMA) of the query encoder \(f_q\). Denoting the parameters of \(f_k\) as \(θ_k\) and those of \(f_q\) as \(θ_q\), we update \(θ_k\) by \(\theta_k \leftarrow m \theta_k + (1-m)\theta_q\), where m = 0.999 is the momentum coefficient. Only the parameters \(θ_q\) are updated by back-propagation during training. The momentum update makes the key encoder evolve more smoothly than the query encoder. With this design, though the keys in the queue are encoded by different encoders (in different mini-batches), the difference among these encoders is small. Therefore we can maintain a sizeable negative sample queue with a stable training process.
Reference
Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick, “Momentum contrast for unsupervised visual representation learning,” in IEEE CVPR, 2020, pp. 9729–9738.